Algebra: Proportions and Cross Multiplying

Proportions and Cross Multiplying

Of all the rational equations you'll see as an algebra student, one of the most common will be the proportion, which is an equation in which two fractions are set equal to one another, like this:

You can solve a proportion just like any other rational function, if you multiply it by the least common denominator of the fractions and simplify. However, there's a quicker and cooler shortcut called cross multiplication that works for proportions only. All you do is multiply each numerator by the denominator of the other fraction and set the results equal, as shown in Figure 18.1.

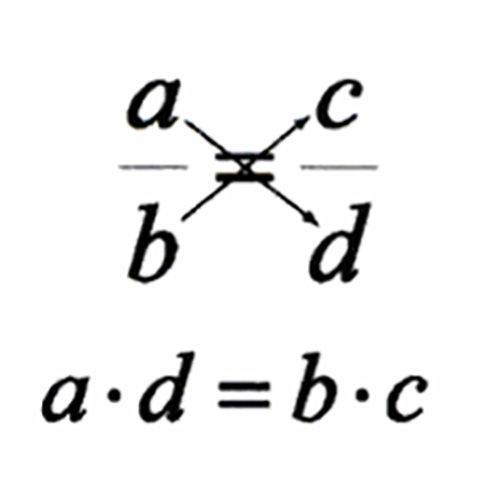
Figure 18.1Cross multiplying eliminates the denominators in a proportion quickly, without the need to calculate a least common denominator.

Example 2: Solve the equation.

Solution: Since this is a proportion, you can cross multiply to eliminate the fractions.

• (x + 3) · 2 = (x - 1)(x + 6)

Distribute the 2 on the left side and multiply the binomials on the right.

• 2x + 6 = x² + 5x - 6

This is a quadratic equation, so set it equal to 0 to try and solve it by factoring.

• x² + 3x - 12 = 0

Nuts€”this bad boy isn't factorable, so you'll have to resort either to completing the square or the quadratic formula to get the solution. (I usually use the quadratic formula, so it doesn't feel like I memorized it for nothing.) You'll end up with a solution of:

Okay, so that wasn't the most attractive problem in the world, but did you notice that the tough part was solving the quadratic equation, not dealing with the fractions? Here's even better news: You don't have to test these (horribly disgusting and unforgivably irrational) answers! Unlike the method you learned earlier in the section, cross multiplication won't introduce possibly false answers that require checking! Huzzah!